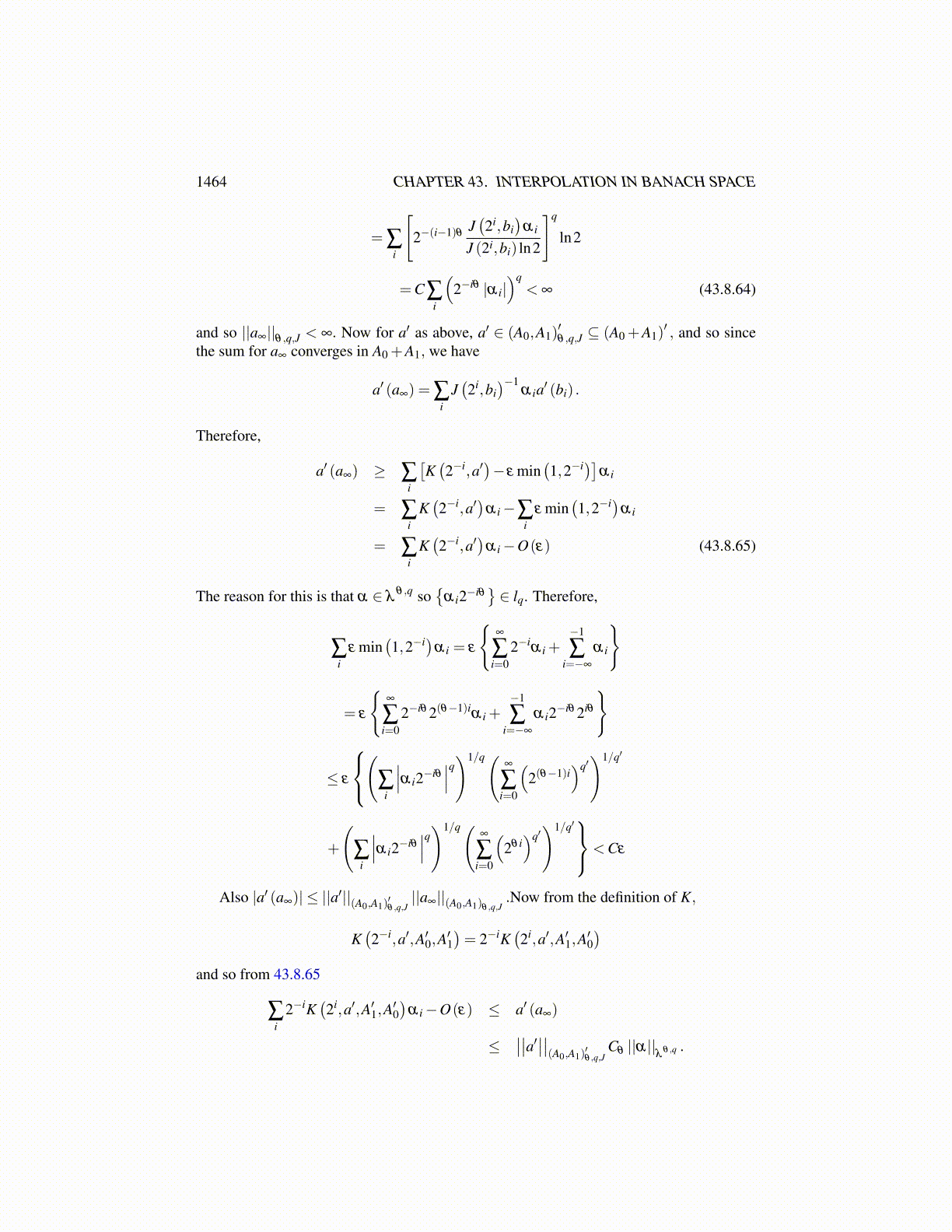
1464 CHAPTER 43. INTERPOLATION IN BANACH SPACE

then a has a representation of the form

a =∫

∞

0u(t)

dtt

where ∫∞

0

(t−θ J (t,u(t))

)q dtt< ∞

whereJ (t,u(t)) = max

(||u(t)||A0

, t ||u(t)||A1

)for u(t) ∈ A0∩A1. Now let

ur (t)≡{

u(t) if t ∈( 1

r ,r)

0 otherwise.

Then∫

∞

0(t−θ J (t,ur (t))

)q dtt < ∞ and

ar ≡∫

∞

0ur (t)

dtt∈ A0∩A1

by Lemma 43.7.2. Also

||a−ar||qθ ,q,J ≤∫ 1

r

0

(t−θ J (t,u(t))

)q dtt+

∫∞

r

(t−θ J (t,u(t))

)q dtt

which is small whenever r is large enough thanks to the dominated convergence theorem.Therefore, A0∩A1 is dense in (A0,A1)θ ,q,J and so

(A0,A1)′θ ,q,J ⊆ (A0∩A1)

′ = A′0 +A′1,

the equality following from Lemma 43.8.1.It follows a′ ∈ A′0 +A′1 and so, by Lemma 43.8.1, there exists bi ∈ A0∩A1 such that

K(2−i,a′,A′0,A

′1)− ε min

(1,2−i)≤ a′ (bi)

J (2i,bi,A0,A1).

Now let α ∈ λθ ,q with α i ≥ 0 for all i and let

a∞ ≡∑i

J(2i,bi,A0,A1

)−1biα i. (43.8.62)

Consider first whether a∞ makes sense before proceeding further.

a∞ ≡∑i

bi2iθ

max(||bi||A0

,2i ||bi||A1

)2−iθα i.