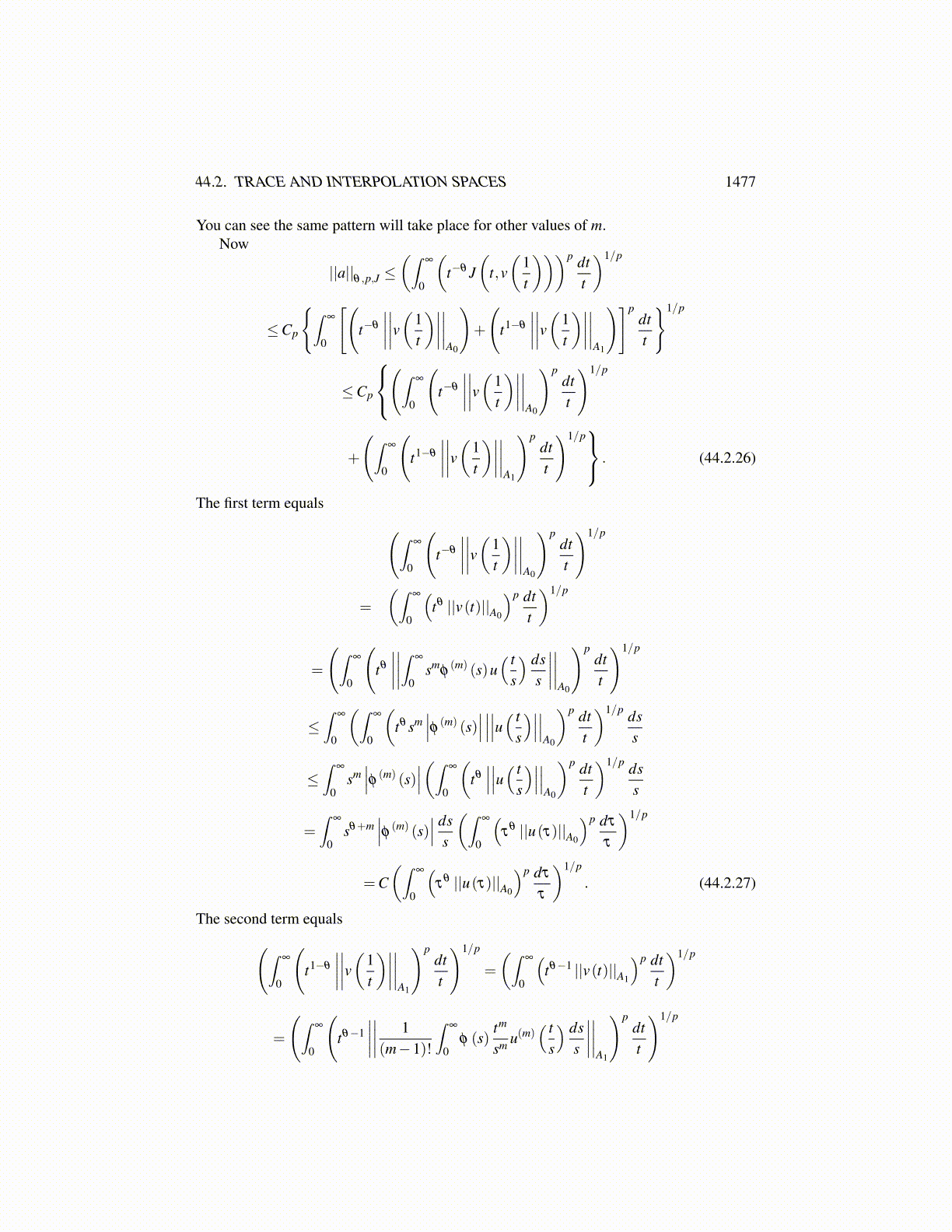
44.2. TRACE AND INTERPOLATION SPACES 1477

The case when m = 1 was discussed in Section 44.1. Note it is not known at this pointwhether limt→0+ u(t) even exists for every u ∈ V m. Of course, if m = 1 this was shownearlier but it has not been shown for m > 1. The following theorem is absolutely amazing.Note the lack of dependence on m of the right side!

Theorem 44.2.3 The following hold.

T m (A0,A1, p,θ) = (A0,A1)θ ,p,J = (A0,A1)θ ,p . (44.2.19)

Proof: It is enough to show the first equality because of Theorem 43.7.5 which identi-fies (A0,A1)θ ,p,J and (A0,A1)θ ,p. Let a ∈ T m. Then there exists u ∈V m such that

a = limt→0+

u(t) in A0 +A1.

The first task is to modify this u(t) to get a better one which is more usable in order toshow a ∈ (A0,A1)θ ,p,J . Remember, it is required to find w(t) ∈ A0 ∩A1 for all t ∈ (0,∞)

and a =∫

∞

0 w(t) dtt , a representation which is not known at this time. To get such a thing,

letφ ∈C∞

c (0,∞) ,spt(φ)⊆ [α,β ] (44.2.20)

with φ ≥ 0 and ∫∞

0φ (t)

dtt= 1. (44.2.21)

Then define

ũ(t)≡∫

∞

0φ

( tτ

)u(τ)

dτ

τ=∫

∞

0φ (s)u

( ts

) dss. (44.2.22)

Claim: limt→0+ ũ(t) = a and limt→∞ ũ(k) (t) = 0 in A0 +A1 for all k ≤ m.Proof of the claim: From 44.2.22 and 44.2.21 it follows that for ||·|| referring to

||·||A0+A1,

||ũ(t)−a|| ≤∫

∞

0

∣∣∣∣∣∣u( ts

)−a∣∣∣∣∣∣φ (s)

dss

=∫

∞

0||u(τ)−a||φ

( tτ

) dτ

τ

=∫ t/α

t/β

||u(τ)−a||φ( t

τ

) dτ

τ

≤∫ t/α

t/β

εφ

( tτ

) dτ

τ= ε

∫β

α

φ (s)dss

= ε

whenever t is small enough due to the convergence of u(t) to a in A0 +A1.Now consider what occurs when t→ ∞. For ||·|| referring to the norm in A0,

ũ(k) (t) =∫

∞

0φ(k)( t

τ

) 1τk u(τ)

dτ

τ