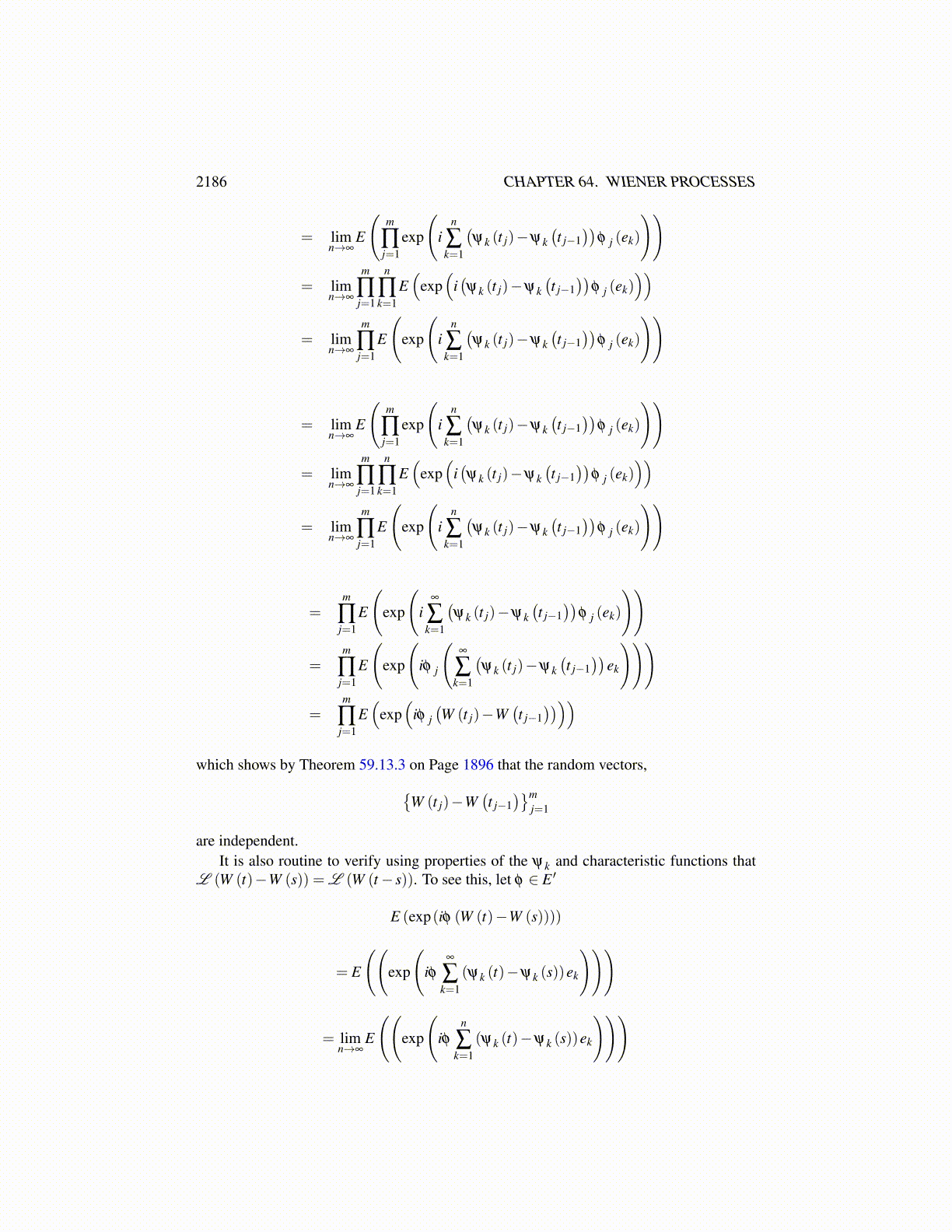
2186 CHAPTER 64. WIENER PROCESSES
Proof: First, there exists a sequence{
ξ i j
}(i, j)∈N×N
such that the{
ξ i j
}are indepen-
dent and each normally distributed with mean 0 and variance 1. This follows from Lemma64.1.2. Let {ξ i}
∞
i=1 be independent and normally distributed with mean 0 and variance 1.(Let θ be a one to one and onto map from N to N×N. Then define ξ i j ≡ ξ
θ−1(i, j).)
Let
ψk (t) =∞
∑j=1
(X[0,t],g j
)L2 ξ k j (64.3.9)
where{
g j}
is a orthonormal basis for L2 (0,∞). By Corollary 64.1.4, this defines a realWiener process satisfying 64.3.8. It remains to show that the random variables
ψkr(tq)−ψkr
(tq−1
)(64.3.10)
are independent.Let
P =n
∑q=1
m
∑r=1
sqr(ψkr
(tq)−ψkr
(tq−1
))and consider E
(eiP). I want to use Proposition 59.11.1 on Page 1891. To do this I need to
show E(eiP)
equals
n
∏q=1
m
∏r=1
E(exp(isqr(ψkr
(tq)−ψkr
(tq−1
)))).
Using 64.3.9, E(eiP)
equals
E
(exp
(i
n
∑q=1
m
∑r=1
sqr
∞
∑j=1
(X[tq−1,tq],g j
)L2
ξ kr j
))
= limN→∞
E
(exp
(i
n
∑q=1
m
∑r=1
sqr
N
∑j=1
(X[tq−1,tq],g j
)L2
ξ kr j
))Now the ξ kr j are independent by construction. Therefore, the above equals
= limN→∞
n
∏q=1
m
∏r=1
N
∏j=1
E(
exp(
isqr
(X[tq−1,tq],g j
)L2
ξ kr j
))
= limN→∞
n
∏q=1
m
∏r=1
N
∏j=1
exp(−1
2s2
qr
(X[tq−1,tq],g j
)2
L2
)
=n
∏q=1
m
∏r=1
limN→∞
exp
(−1
2s2
qr
N
∑j=1
(X[tq−1,tq],g j
)2
L2
)
=n
∏q=1
m
∏r=1
exp(−1
2s2
qr(tq− tq−1
))