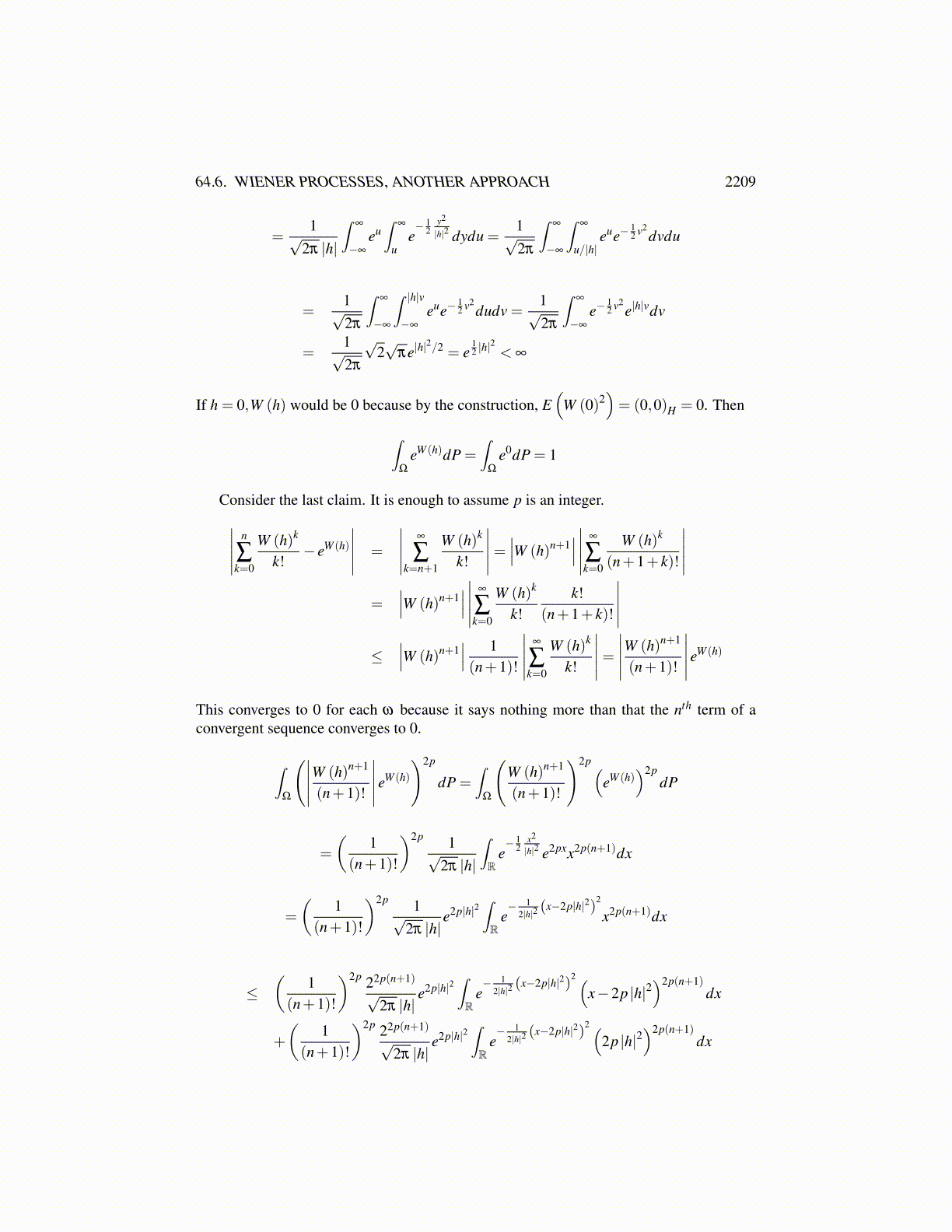
64.6. WIENER PROCESSES, ANOTHER APPROACH 2209

Lemma 64.6.3 Let X ≥ 0 and measurable. Also define a finite measure on B (Rp)

ν (B)≡∫

Ω

XXB (Y)dP

Then let f : Rp→ [0,∞) be Borel measurable. Then∫Ω

f (Y)XdP =∫Rp

f (y)dν (y)

where here Y is a given measurable function with values in Rp. Formally, XdP = dν .

Note that Y is given and X is just some random variable which here has nonnegativevalues. Of course similar things will work without this stipulation.

Proof: First say X = XD and replace f (Y) with XY−1(B). Then∫Ω

XDXY−1(B)dP = P(D∩Y−1 (B)

)∫Rp

XB (y)dν (y) ≡ ν (B)≡∫

Ω

XDXB (Y)dP

=∫

Ω

XDXY−1(B)dP = P(D∩Y−1 (B)

)Thus ∫

Ω

XDXY−1(B)dP =∫

Ω

XDXB (Y)dP =∫Rp

XB (y)dν (y)

Now let sn (y) ↑ f (y) , and let sn (y) = ∑mk=1 ckXBk (y) where Bk is a Borel set. Then∫

Rpsn (y)dν (y) =

∫Rp

m

∑k=1

ckXBk (y)dν (y) =m

∑k=1

ck

∫Rp

XBk (y)dν (y)

=m

∑k=1

ckP(D∩Y−1 (Bk)

)∫

Ω

sn (Y)XDdP =m

∑k=1

ck

∫Ω

XDXBk (Y)dP =m

∑k=1

ckP(D∩Y−1 (Bk)

)which is the same thing. Therefore,∫

Ω

sn (Y)XDdP =∫Rp

sn (y)dν (y)

Now pass to a limit using the monotone convergence theorem to obtain∫Ω

f (Y)XDdP =∫Rp

f (y)dν (y)

Next replace XD with ∑mk=1 dkXDk ≡ sn (ω) , a simple function.∫

Ω

f (Y)m

∑k=1

dkXDk dP =m

∑k=1

dk

∫Ω

f (Y)XDk dP