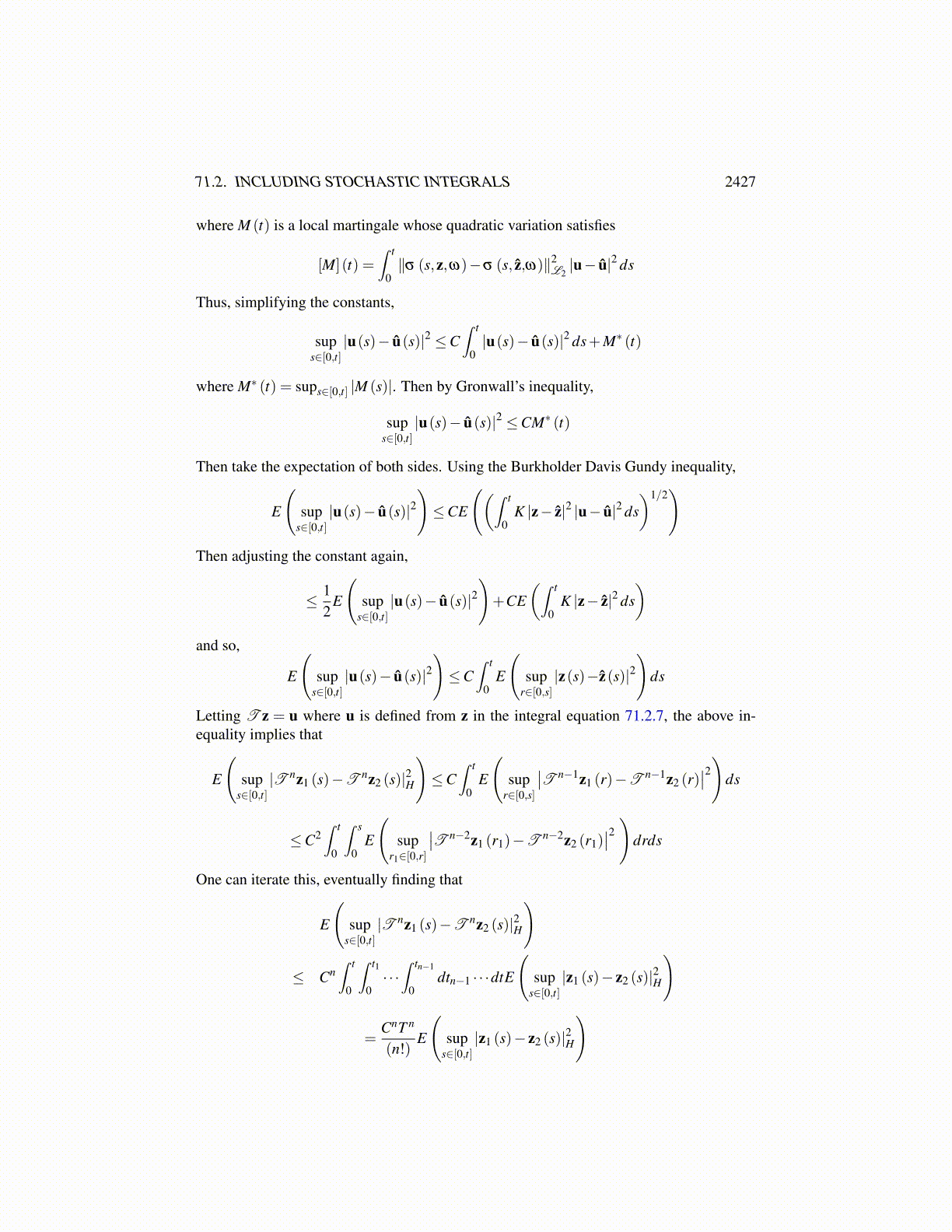
71.2. INCLUDING STOCHASTIC INTEGRALS 2427
is progressively measurable with respect to the normal filtration Ft determined by a givenWiener process W (t). Also suppose
(t,u,v,w)→ N(t,u,v,w,ω)
is continuous and satisfies the following conditions for C (·,ω)≥ 0 in L1 ([0,T ]) and someµ > 0:
(N(t,u,v,w,ω) ,u)≥−C (t,ω)−µ
(|u|2 + |v|2 + |w|2
). (71.2.3)
Also let f be progressively measurable and f(·,ω) ∈ L2([0,T ] ;Rd
). Let
Φ ∈ L2([0,T ]×Ω;L2
(Q1/2U,Rd
))where U is some Hilbert space, Rd , for example. Also suppose path uniqueness. That is,for each ω, there is at most one solution to the integral equation
u(t,ω)−u0(ω)+∫ t
0N(s,u(s,ω),u(s−h,ω) ,w(s,ω) ,ω)ds
=∫ t
0f(s,ω)ds+
∫ t
0ΦdW, (71.2.4)
Then for h > 0, there exists a unique progressively measurable solution u to the integralequation 71.2.4 where u0 has values in Rd and is F0 measurable. Here u(s−h,ω) ≡u0 (ω) for all s−h≤ 0 and for w0 a given F0 measurable function,
w(t,ω)≡ w0 (ω)+∫ t
0u(s,ω)ds
Proof: The only thing left is to observe that the given estimate is sufficient to obtain anestimate for the solutions to the integral equation for û defined above. Then from Theorem71.1.1, there exists a unique progressively measurable solution for û and hence for u.
Note that the integral equation holds for all t for each ω . There is no exceptional set ofmeasure zero which might depend on the initial condition needed.
What is a sufficient condition for path uniqueness? Suppose the following weak mono-tonicity condition for µ = µ (ω) .
(N(t,u1,v1,w1,ω)−N(t,u2,v2,w2,ω) ,u1−u2)
≥ −µ
(|u1−u2|2 + |v1−v2|2 + |w1−w2|2
)(71.2.5)
Then path uniqueness will hold. This follows from subtracting the two integral equations,one for u1 and one for u2, using the estimate and then applying Gronwall’s inequality.
Recall the Ito formula
u(t)−u0 +∫ t
0Nds =
∫ t
0f ds+
∫ t
0ΦdW