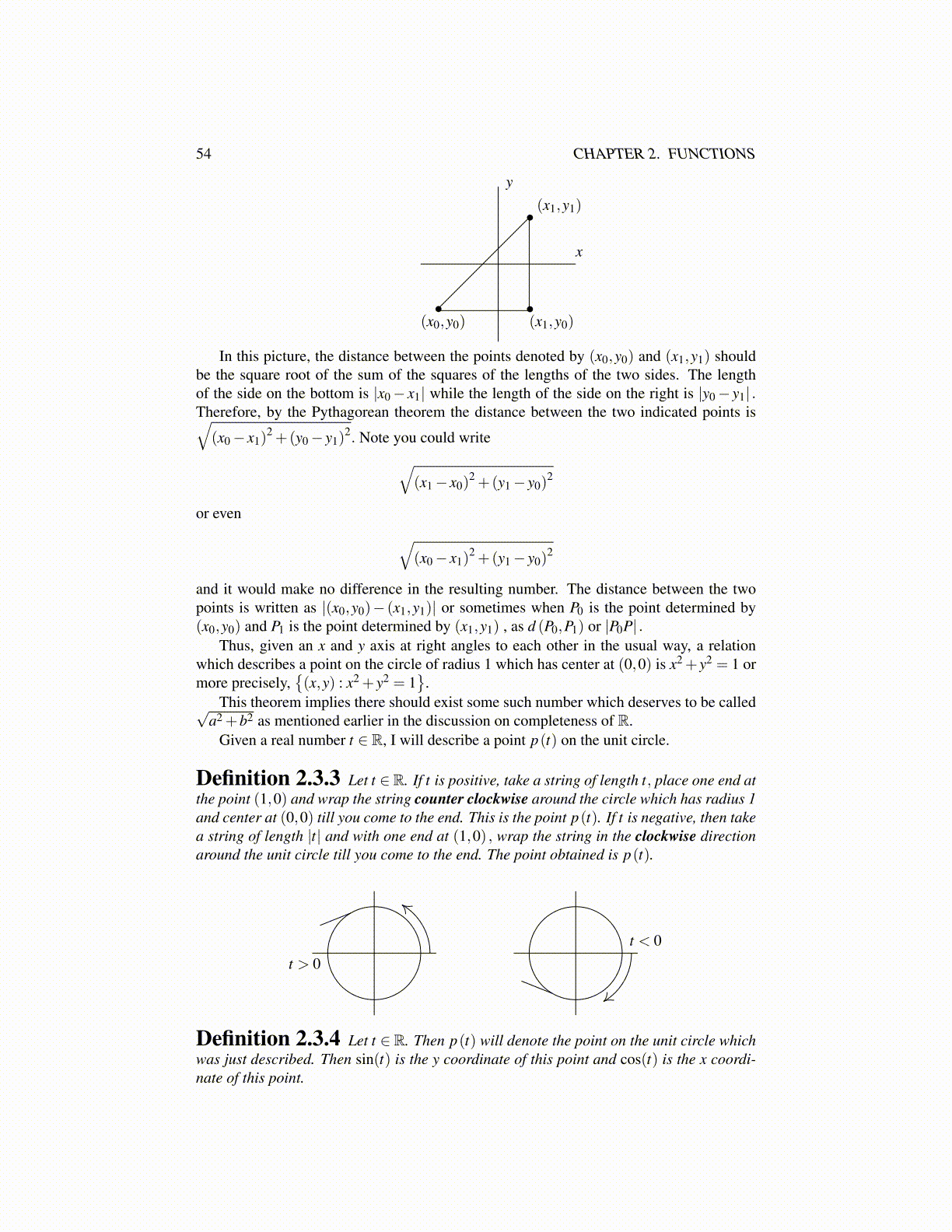
54 CHAPTER 2. FUNCTIONS

y

x

•

•

(x1,y1)

(x0,y0) (x1,y0)•

In this picture, the distance between the points denoted by (x0,y0) and (x1,y1) shouldbe the square root of the sum of the squares of the lengths of the two sides. The lengthof the side on the bottom is |x0 − x1| while the length of the side on the right is |y0 − y1| .Therefore, by the Pythagorean theorem the distance between the two indicated points is√(x0 − x1)

2 +(y0 − y1)2. Note you could write√

(x1 − x0)2 +(y1 − y0)

2

or even √(x0 − x1)

2 +(y1 − y0)2

and it would make no difference in the resulting number. The distance between the twopoints is written as |(x0,y0)− (x1,y1)| or sometimes when P0 is the point determined by(x0,y0) and P1 is the point determined by (x1,y1) , as d (P0,P1) or |P0P| .

Thus, given an x and y axis at right angles to each other in the usual way, a relationwhich describes a point on the circle of radius 1 which has center at (0,0) is x2 +y2 = 1 ormore precisely,

{(x,y) : x2 + y2 = 1

}.

This theorem implies there should exist some such number which deserves to be called√a2 +b2 as mentioned earlier in the discussion on completeness of R.

Given a real number t ∈ R, I will describe a point p(t) on the unit circle.

Definition 2.3.3 Let t ∈R. If t is positive, take a string of length t, place one end atthe point (1,0) and wrap the string counter clockwise around the circle which has radius 1and center at (0,0) till you come to the end. This is the point p(t). If t is negative, then takea string of length |t| and with one end at (1,0) , wrap the string in the clockwise directionaround the unit circle till you come to the end. The point obtained is p(t).

t > 0t < 0

Definition 2.3.4 Let t ∈ R. Then p(t) will denote the point on the unit circle whichwas just described. Then sin(t) is the y coordinate of this point and cos(t) is the x coordi-nate of this point.