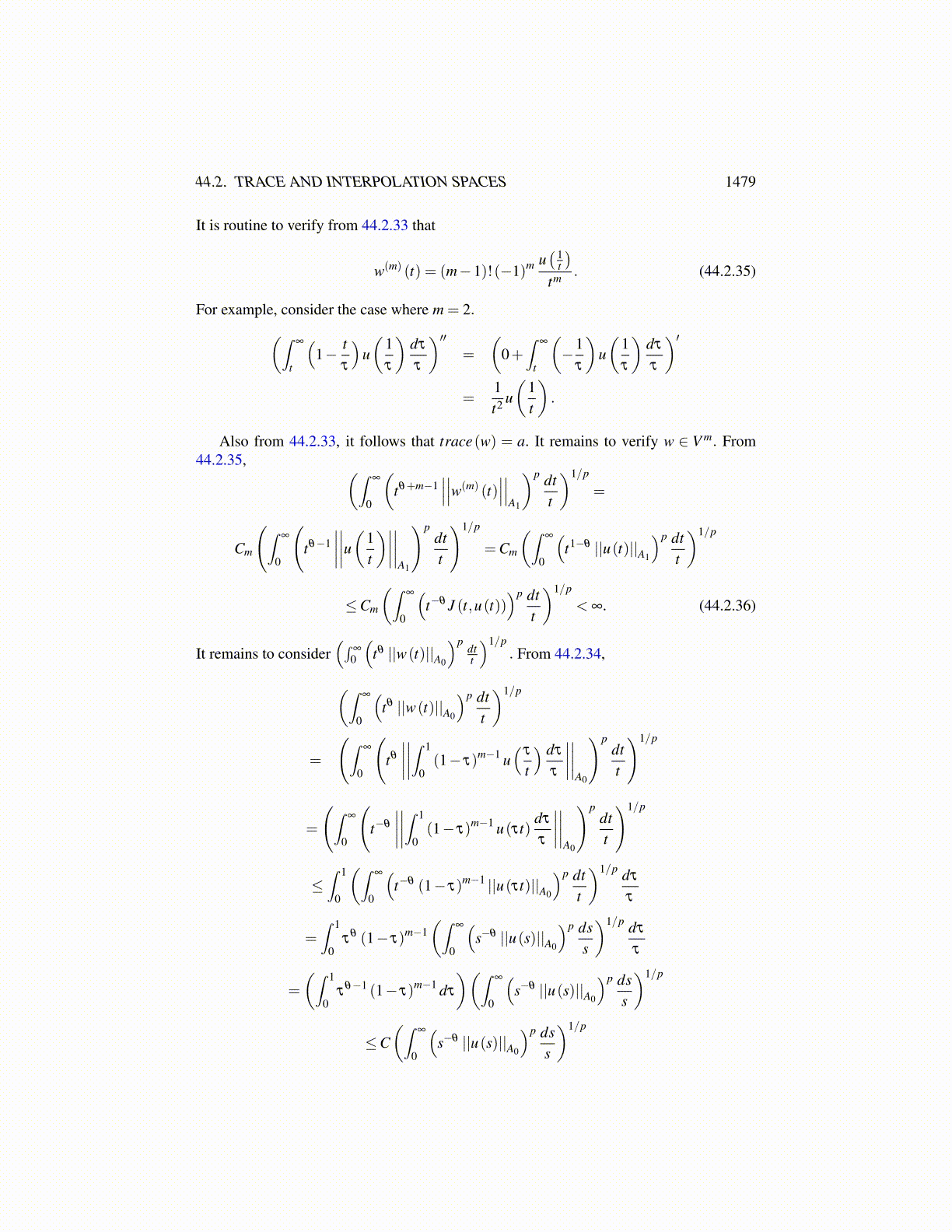
44.2. TRACE AND INTERPOLATION SPACES 1479
You can see the same pattern will take place for other values of m.Now
||a||θ ,p,J ≤
(∫∞
0
(t−θ J
(t,v(
1t
)))p dtt
)1/p
≤Cp
{∫∞
0
[(t−θ
∣∣∣∣∣∣∣∣v(1t
)∣∣∣∣∣∣∣∣A0
)+
(t1−θ
∣∣∣∣∣∣∣∣v(1t
)∣∣∣∣∣∣∣∣A1
)]pdtt
}1/p
≤Cp
(∫
∞
0
(t−θ
∣∣∣∣∣∣∣∣v(1t
)∣∣∣∣∣∣∣∣A0
)pdtt
)1/p
+
(∫∞
0
(t1−θ
∣∣∣∣∣∣∣∣v(1t
)∣∣∣∣∣∣∣∣A1
)pdtt
)1/p . (44.2.26)
The first term equals (∫∞
0
(t−θ
∣∣∣∣∣∣∣∣v(1t
)∣∣∣∣∣∣∣∣A0
)pdtt
)1/p
=
(∫∞
0
(tθ ||v(t)||A0
)p dtt
)1/p
=
(∫∞
0
(tθ
∣∣∣∣∣∣∣∣∫ ∞
0sm
φ(m) (s)u
( ts
) dss
∣∣∣∣∣∣∣∣A0
)pdtt
)1/p
≤∫
∞
0
(∫∞
0
(tθ sm
∣∣∣φ (m) (s)∣∣∣ ∣∣∣∣∣∣u( t
s
)∣∣∣∣∣∣A0
)p dtt
)1/p dss
≤∫
∞
0sm∣∣∣φ (m) (s)
∣∣∣(∫ ∞
0
(tθ
∣∣∣∣∣∣u( ts
)∣∣∣∣∣∣A0
)p dtt
)1/p dss
=∫
∞
0sθ+m
∣∣∣φ (m) (s)∣∣∣ ds
s
(∫∞
0
(τ
θ ||u(τ)||A0
)p dτ
τ
)1/p
=C(∫
∞
0
(τ
θ ||u(τ)||A0
)p dτ
τ
)1/p
. (44.2.27)
The second term equals(∫∞
0
(t1−θ
∣∣∣∣∣∣∣∣v(1t
)∣∣∣∣∣∣∣∣A1
)pdtt
)1/p
=
(∫∞
0
(tθ−1 ||v(t)||A1
)p dtt
)1/p
=
(∫∞
0
(tθ−1
∣∣∣∣∣∣∣∣ 1(m−1)!
∫∞
0φ (s)
tm
sm u(m)( t
s
) dss
∣∣∣∣∣∣∣∣A1
)pdtt
)1/p